Question

Point J(8, 5) was translated as follows: J(8, 5) J’(2, 9). A student wrote the algebraic rule to describe the translation as . Evaluate the student’s answer. A. Incorrect; the student should add 8 + 2 to calculate the x-coordinate and should add 5 + 9 to calculate the y-coordinate. B. Incorrect; the student added 4 to the y-coordinate instead of subtracting 4 from the y-coordinate. C. Incorrect; the student added 6 to the x-coordinate instead of subtracting 6 from the x-coordinate. OF. The student’s answer is correct.

Answer 1

`(x,y)\rightarrow (x-6,y+4)`

Explanation:

The rule of translation is defined as

`P(x,y)\rightarrow P'(x+a,y+b)`

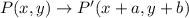
where, a is horizontal shift and b is vertical shift.

The given point is J(8,5). After a translation the image of point J is J'(2,9).

`J(8,5)\rightarrow J'(8+a,5+b)`

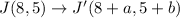
The image of point J is J'(2,9).

`J'(8+a,5+b)=J'(2,9)`

On comparing both sides we get

`8+a=2`

`a=2-8`

`a=-6`

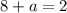
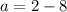
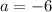
The value of a is -6.

`5+b=9`

`b=9-5`

`b=4`

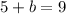
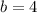
The value of b is 4.

The rule of translation is

`(x,y)\rightarrow (x-6,y+4)`

It means 6 should be subtracted from x-coordinate and 4 should be added to the y-coordinate.