Answer: Probability of the arrow landing on a green colored section is

Explanation:
Since we have given that
Probability of the arrow landing on a section colored blue =
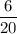
Probability of the arrow landing on a section colored red =
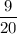
Since there are only three sections i.e. red, blue and green.
We need to find the probability of the arrow landing on a section colored green.
Required probability is given by
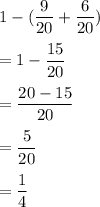
Hence, Probability of the arrow landing on a green colored section is
