Question

How many permutations exist of the letters a, b, c, d taken four at a time?

A.24
B. 12
C. 4

Answer 1

The correct answer is A) 24

4*3*2*1=24

Answer 2

A. 24

Explanation:

We are asked to find the number of permutations exist of the letters a, b, c, d taken four at a time.

We will use permutation formula to solve our given problem.

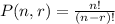`P(n,r)=(n!)/((n-r)!)`, where,

n = Total number of objects,

r = Number of objects taken at a time.

We can see total number of letters is 4 and number of letters taken at a time is also 4, so substituting these values in permutation formula we will get,

`P(4,4)=(4!)/((4-4)!)`

`P(4,4)=(4!)/((0)!)`

`P(4,4)=(4!)/(1)`

`P(4,4)=(4*3*2*1)/(1)`

`P(4,4)=(24)/(1)`

`P(4,4)=24`

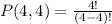
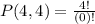
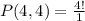
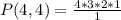
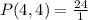
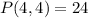
Therefore, 24 permutations exist for our given letters and option A is the correct choices.