Question

The excluded values of a rational expression are –3, 0, and 8. Which of the following could be this expression?

Answer 1

Excluded values are -3, 0 and 8, so denominator will be:


`(x-(-3))\cdot(x-0)\cdot(x-8)=(x+3)\cdot x\cdot(x-8)=(x+3)(x-8)x=\\\\=(x^2-8x+3x-24)x=(x^2-5x-24)x=\boxed{x^3-5x^2-24x}`

Answer A.

Answer 2

The correct option is 1.

Explanation:

If a rational function is defined as

`R(x)=(P(x))/(Q(x))`

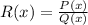
then the excluded values of a rational expression are zeroes of the denominator. In other words, the excluded values of a rational expression are those values of x for which Q(x)=0.

It is given that the excluded values of a rational expression are –3, 0, and 8. It means denominator have three zeroes or degree 3.

Only expression 1 has denominator with degree 3. The first expression is

`(x+2)/(x^3-5x^2-24x)`

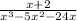
Equate denominator equal to 0.

`x^3-5x^2-24x=0`

The roots of this equation are excluded values of the rational expression.

Taking out the common factor.

`x(x^2-5x-24)=0`

`x(x^2-8x+3x-24)=0`

`x(x(x-8)+3(x-8))=0`

`x(x+3)(x-8)=0`

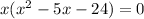
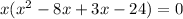
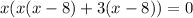
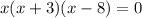
Using zero product property, we get

`x=0`

`x+3=0\Rightarrow x=-3`

`x-8=0\Rightarrow x=8`

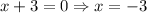
The excluded values of first rational expression are –3, 0, and 8. Theretofore the correct option is 1.