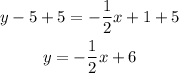To determine the equation of a line perpendicular to y=2x-2 that passes through the point (2,5) you need to determine the slope of the line first.
If two lines are perpendicular, their slopes are negative reciprocals from each other. For example, if we have the lines:
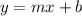
and
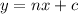
That are perpendicular, then their slopes have the following relation:
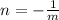
Following this, the slope of the given line is the coefficient that multiplies the x term:
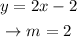
The negative reciprocal of m=2 will be the slope of the perpendicular line:
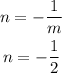
Now that we have determined the slope of the line we are looking for, using the point-slope form we can determine the equation of the perpendicular line:
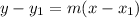
Where
(x₁,y₁) are the coordinates of one point of the line
m is the slope of the line
Using m=-1/2 for the slope and coordinates (2,5) the equation of the line is
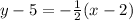
Now you have to express it in slope-intercept form. First, distribute the multiplication on the right side of the equation:
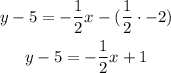
Then pass 5 to the other side of the equation by applying the opposite operation