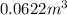Answer:
The volume of the submerged part of her body is
Step-by-step explanation:
Let's define the buoyant force acting on a submerged object.
In a submerged object acts a buoyant force which can be calculated as :
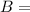 ρ.V.g
ρ.V.g
Where ''B'' is the buoyant force
Where ''ρ'' is the density of the fluid
Where ''V'' is the submerged volume of the object
Where ''g'' is the acceleration due to gravity
Because the girl is floating we can state that the weight of the girl is equal to the buoyant force.
We can write :
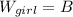 (I)
(I)
Where ''W'' is weight
⇒ If we consider ρ =
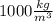 (water density) and
(water density) and
 and replacing this values in the equation (I) ⇒
and replacing this values in the equation (I) ⇒

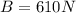
ρ.V.g = 610N
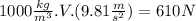 (II)
(II)
The force unit ''N'' (Newton) is defined as
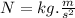
Using this in the equation (II) :

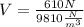
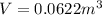
We find that the volume of the submerged part of her body is