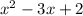Question

The width, w, of a rectangular playground is x +3 . The area of the playground is x^3-7x+6 . What is an expression for the length of the playground? (1 point)

Answer 1

To find the length of the playground, you multiply length(width) = area

To reverse this, you have to divide on each side by the term we know (x + 3)

The answer would be width = (x³ - 7x + 6) / (x + 3)

If you need help solving this, let me know

Answer 2

Length is :
`x^(2) -3x+2`

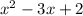
Explanation:

The width of the rectangular playground is given as = x+3

The area of the playground is given as =
`x^(3) -7x+6`

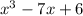
We have to find the length.

The area of the rectangle is given as :

`A= length*width`

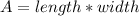
So, length can be found as :
`length=(area)/(width)`

=>
`(x^(3)-7x+6 )/(x+3)`

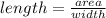
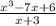
Solving this we get,

Factoring
`\frac{x^(3)-7x+6 }` we get (x-1)(x-2)(x+3)

Using the rational root theorem and assuming a0=6 and a(n)=1

Divisors of a0 = 1,2,3,6

Divisor of a(n) = 1

1/1 is the root of equation. So, factoring out x-1 we get

`(x-1)(x^(3)-7x+6 )/(x-1)`

`(x^(3)-7x+6 )/(x-1)`

`x^(2) +(x^(2)-7x+6 )/(x-1)`

`x^(2) +x+(-6x+6)/(x-1)`

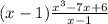
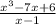
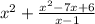
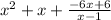
dividing
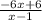`(-6x+6)/(x-1)` we get -6

So, result becomes
`x^(2) +x-6`

Factoring this we get:
`(x-2)(x+3)`

`((x-1)(x-2)(x+3))/((x+3))`

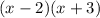
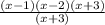
Cancelling x+3

We get the length as =
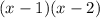`(x-1)(x-2)` or
`x^(2) -3x+2`