
Step-by-step explanation
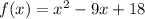
Step 1
a)Domain:
The domain of a function is the set of all possible inputs for the function, in other words, the values that x can take, so
there is no restriction for this function, hence, the domain is all real numbers
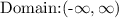
b)Range: is the set of all possible values that the function will give when we give in the domain as input
to know the range of a quadratic equation, do
a) set the function equals zero
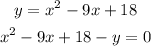
now, we need to solve for x, use the quadratic formula
let
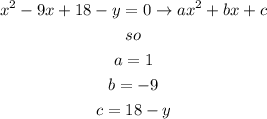
apply the formula
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-9)\pm\sqrt[]{(-9)^2-4(1)(18-y)}}{2\cdot1} \\ x=\frac{+9\pm\sqrt[]{81-72+4y}}{2} \\ x=\frac{+9\pm\sqrt[]{9+4y}}{2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/bq10zqmdrylu8kgq3gse.png)
now, this has solution only if the value insides the roor sign, is greater or equal than zero,so

hence, the range is
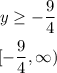
Step 2
extremes A quadratic function f(x)=ax2+bx+c has an extreme value at its vertex, so if a>0 , then f(−ba) is the maximum, and if a<0
so
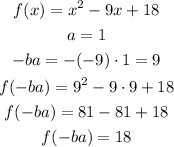
so, extrema=18
Zeros: the zeros of a function is the values where the line intersect the y and x-axis, so
a) set the function to zero and solve
![\begin{gathered} x^2-9x+18=0 \\ x=\frac{-(-9)\pm\sqrt[]{(-9)^2-4\cdot1\cdot18}}{2\cdot1} \\ x=\frac{9\pm\sqrt[]{81-72}}{2} \\ x=\frac{9\pm\sqrt[]{9}}{2} \\ x=(9\pm3)/(2) \\ x_1=(9+3)/(2)=(12)/(2)=6 \\ x_2=(9-3)/(2)=(6)/(2)=3 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/qfr9bpn6be7y2v2obbw1.png)
hence, the graph intersectsmy p the x axis at, x= 3 and x= 6
now, the y -intercetp is when the line intersecnt the y -axis, it ocurrs when x= 0, so evalute at x=0
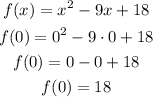
it means, the graph intersect the y-axis at y=18
y-intercept:18
Step 3
increasing and decreasing
a) derivate the function and equals to zero
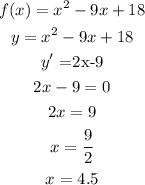
it means the inflection point is x=4.5
b) now, get the second derivate of the function to check its behavior ( if y'' is greater than zero, the function open upwards)
![\begin{gathered} y^(\prime)\text{ =2x-9} \\ y^(\doubleprime)=\text{ 2} \\ 2>0,\text{ so the graph open upwards} \end{gathered}]()
hence
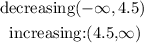
c) Continuity:
as the domain is all the real numbers the function is totally continuos
I hope this helps you