Answer:
127512000 ways
Explanation:
Total number of students = 25
and number of medals to be distributed = 6 for first six place
Since order of medals [six place] matters
then permutation will be applied to calculate the different ways in which medals can be awarded.
Number of ways =
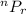
where n = 25 and r = 6
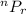 =
=
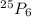 =
=
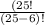
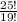
= 25 × 24 × 23 × 22 × 21 × 20
= 127512000 ways