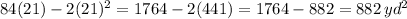Let x denote the length of the side of the garden which is covered fenced by a shed, and

be the width of the garden.
The perimeter of a rectangle is given by 2(length + width)
i.e.
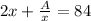
which gives:
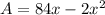
For the area to be maximum, the differentiation of A with respect to x must be equal to 0.
i.e.
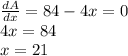
Therefore, the maximum area of the garden enclosed is given by