Question

A King in ancient times agreed to reward the inventor of chess with one grain of wheat on the first of the 64 squares of a chess board. On the second square the King would place two grains of​ wheat, on the third​ square, four grains of​ wheat, and on the fourth square eight grains of wheat. If the amount of wheat is doubled in this way on each of the remaining​ squares, how many grains of wheat should be placed on square 15? Also find the total number of grains of wheat on the board at this time and their total weight in pounds.​ (Assume that each grain of wheat weighs​ 1/7000 pound.)

Answer 1

16,384 grains should be on square 15. The total number of grains at this point should be 32,767, as the pattern seems to be that the sum of the numbers before it will be one less than it; that means, then, that the total number of grains is 16,384+16,383. The weight, assuming each grain weighs 1/7000 pound, is 4.681 pounds, or a bit less than 4 pounds 11 ounces.

Answer 2

Let's start by visualising this concept.

Number of grains on square:
1 2 4 8 16 ...

We can see that it starts to form a geometric sequence, with the common ratio being 2.

For the first question, we simply want the fifteenth term, so we just use the nth term geometric form:

`T_n = ar^(n - 1)`

`T_(15) = 2^(14) = 16384`

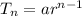
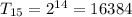
Thus, there are 16, 384 grains on the fifteenth square.

The second question begs the same process, only this time, it's a summation. Using our sum to n terms of geometric sequence, we get:

`S_n = (a(r^(n) - 1))/(r - 1)`

`S_(15) = (2^(15) - 1)/(2 - 1)`

`S_(15) = 2^(15) - 1 = 32767`

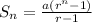
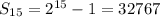
Thus, there are 32, 767 total grains on the first 15 squares, and you should be able to work the rest from here.