Question

In a student government election, 6 seniors, 2 juniors, and 3 sophomores are running for election. Students elect four at-large senators. In how many ways can this be done?

Answer 1

4-0-0
2-1-1
1-2-1
1-0-3
0-1-3


Those are just the ones I can think of so about 5 ways

Answer 2

330 ways.

Explanation:

4 senators of 11 people should be selected, that is a combination of the C(n,r) form, where

n = 11

r = 4

That's C(11,4)

The combinations form uses factorial numbers. This is the formula:

`C(n,r)=(n!)/((n-r)! r!)`

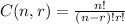
Substituting the variables for their respective data, we have

`C(11,4)=(11!)/((11-4)! 4!)`

`C(11,4)=(11.10.9.8.7!)/(7! 4!)`

`C(11,4)=(11.10.9.8)/(4!)`

`C(11,4)=(11.10.9.8)/(4.3.2)`

`C(11,4)=(7920)/(24)`

`C(11,4)=330`

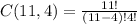
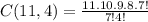
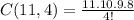
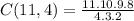
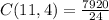
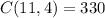
Students can elect four at-large senators of 330 ways.

Hope this helps!