Question

A real estate agent is working for a developer who claims that the average commute time to downtown is 20 minutes with a standard deviation of 7 minutes. Stephon is an independent real estate agent and wants to check the times for his client. He took a random sample of 15 commute times and found an average of 26 minutes. He did hypothesis testing using a significance level of 5%. Which conclusion could he make?

The z-statistic is 0.22, so the null hypothesis should not be rejected.
The z-statistic is 1.69, so the null hypothesis should not be rejected.
The z-statistic is 3.32, so the null hypothesis should be rejected.
The z-statistic is 3.67, so the null hypothesis should be rejected.

Answer 1

Answer: the answer is c

Explanation:

Answer 2

To conduct a hypothesis test for the above situation. We define the null hypothesis and the alternative hypothesis.

The null hypothesis is the claim that the average commute time to downtown is 20 minutes while the alternative hypotheis is a contradiction of the null hypothesis which is that the average commute time to downtown is not 20 minutes.
i.e. H0: μ = 20 and H1: μ ≠ 20.

The z-statistics is given by (sample mean - hypothesized mean) divided by (standard deviation divided by the square root of the sample size).
i.e.

`z= \frac{\bar{x}-\mu}{\sigma/ √(n) } \\ where:\bar{x}=26, \ \mu=20, \ \sigma=7, \ and \ n=15 \\ z= (26-20)/(7/ √(15) ) = (6)/(1.807) =3.32`

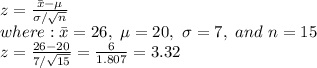
Therefore, The z-statistic is 3.32, so the null hypothesis should be rejected. Because the calculated value of z (3.32) is greater than the table value of z (1.96).

*The table value of z is the z (alpha / 2) of the significant level.