Question

An electronics store is deciding how to price one of its products. The equation P=-25d^2+500d predicts the total profit P as a function of the product's price in dollars d. What price will produce the highest total profit?

Answer 1

1. The function calculating the profit in terms of the price in dollars d, is the quadratic function
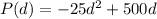
`P(d)=- 25d^(2)+500d`, whose graph is a concave parabola, that is a parabola which opens downwards, because the coefficent of
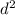
`d^(2)` is negative.

2. The function P takes its maximum value at the vertex, so we want to find the x coordinate of the vertex.

3.
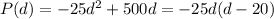
`P(d)=- 25d^(2)+500d=-25d(d-20)` is the factorized form of the function P, which clearly gives the roots (solutions) 0 and 20 of P(d)=0, which are the x intercepts of the parabola.

4. The axis of symmetry, which contains the vertex, is the vertical line passing through the point equidistant to 0 and 20, that is 10.

5. Remark : The vertex is (10, P(10))=(10, -25*10(10-20))=(10, 2500)

So for price d=10 dollars, the (expected) Profit is 2500 dollars.

6. Remark 2. The x coordinate is also found by the formula -b/2a, where b is the coefficient of the linear term, and a the coefficient of the quadratic term of a quadratic expression. So in our case -b/2a=-500/2(-25)=-500/-50=10