hello
to solve this problem, we need the formula of length of an arc
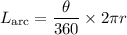
t find the value of angle JM, we should take into cognizance that the sum of angles in a circle is equal to 360 degree and angle on a straight line is equal to 180 degree
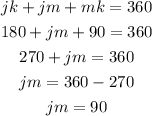
now we know the value of angle jm, let's find the length of the radius

with all the necessary informations or data required, we can now proceed to solve for the length of arc jm
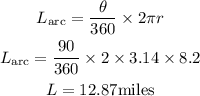
from the calculations above, the length of the arc is equals to 12.87 miles