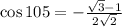Question

Hi, teacher I was absent these days and I didn’t understand anything about this lesson and I need help this is not count as a test it’s just hw please help thanks a lot The first question

Answer 1

The half formula for the cosine is as follows:

`\cos(\theta)/(2)=\pm\sqrt{(1+\cos\theta)/(2)}`

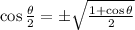
So, using 210°, we will be able to find 105°, which is half of 210°:

Now, we just need to figure the sign out.

The cosine gives positive values for the first and fourth quadrant and gives negative values for the second and third quadrants. The angle 105° is between 90° and 180°, which means it is in the second quadrant and its cosine can only be negative.

Thus, the exact value is:

We can simplify a bit by trying to make a binomial square inside the first square root.

The goal is to have something like:

`(√(3)-b)^2=3-2b√(3)+b^2`

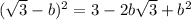
To make this work, we can, for instance, multiply the inside of the root by 2/2, which won't change its value, by will make a 2 appear on the square root of 3:

`\cos105\degree=-\frac{\sqrt{2-√(3)}}{2}=-\frac{\sqrt{(4-2√(3))/(2)}}{2}=-\frac{\sqrt{(3-2√(3)+1)/(2)}}{2}=-\frac{\sqrt{((√(3)-1)^2)/(2)}}{2}=-\frac{\frac{\sqrt{(√(3)-1)^2}}{√(2)}}{2}=-\frac{\sqrt{(√(3)-1)^2}}{2√(2)}`

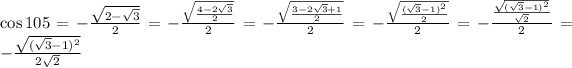
Now, we can cancel the square root and the square, but this makes us have to consider again both + and - possibilities:

`\cos105\degree=\pm(√(3)-1)/(2√(2))`

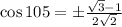
Again, we know that the value of this cosine has to be negative. The way it is, both the numerator and the denominator are positive, so for the cosine to be negative the front sign has to be negative.

So, the final value is:

`\cos105\degree=-(√(3)-1)/(2√(2))`