Answer:
The range of the function is {9.5,7.5,4.5,2.5,1.5}.
Explanation:
Given : The domain of the function
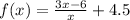 is {-3,-1,2,4,5}.
is {-3,-1,2,4,5}.
To find : The range of the function ?
Solution :
Function
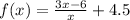
Domain of the function {-3,-1,2,4,5}.
Range is defined as the set of values that corresponds with the domain.
To find the range we put all values of x to get f(x),
Put x=-3,
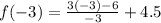
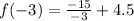
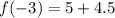
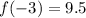
Put x=-1,
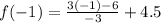

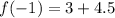
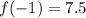
Put x=2,
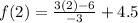
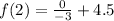
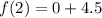
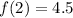
Put x=4,
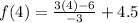
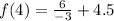
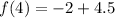
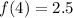
Put x=5,
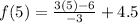

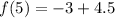
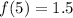
Therefore, The range of the function is {9.5,7.5,4.5,2.5,1.5}.