Question

A leading dental journal claims that 68% of young adults do not brush their teeth regularly. A dental hygienist wants to conduct a survey to verify this with her young adult patients, and wants to do so with a margin of error (ME) of ± 5%. What minimum sample size, rounded to the nearest whole person, does the hygienist need to use? Hint: ME equals plus or minus two times square root of start fraction p hat left parenthesis one minus p hat right parenthesis over N end fraction end square root, where p hat is the yes proportion in the sample and N is the sample size N ≥ 175 N ≥ 348 N ≥ 366 N ≥ 400

Answer 1

To calculate the minimum sample size needed to conduct a survey to verify the claim that 68% of young adults do not brush their teeth regularly.

The sample size for a proportion estimation is given by

`n= ((z_( \alpha /2)√(p(1-p)))/(ME) )^2`
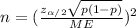
where:
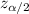
`z_( \alpha /2)` is the z-score of the confidence level and p is the proportion being tested.

Setting our confidence level to be 95%, then
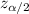
`z_( \alpha /2)` = 1.96

Thus,

`n= ((1.96*√(0.68(1-0.68)))/(0.05) )^2 \\ = ((1.96* √(0.2176) )/(0.05))^2= ((1.96(0.466476))/(0.05))^2 \\ = ((0.914293)/(0.05) )^2=(18.2859)^2=335`
i.e. N ≥ 335.

Setting our confidence level to be 90%, then
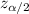`z_( \alpha /2)` = 1.645

Thus,

`n= ((1.645*√(0.68(1-0.68)))/(0.05) )^2 \\ = ((1.645* √(0.2176) )/(0.05))^2= ((1.645(0.466476))/(0.05))^2 \\ = ((0.767353)/(0.05) )^2=(15.3471)^2=236`
i.e. N ≥ 236.


Setting our confidence level to be 99%, then
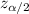`z_( \alpha /2)` = 2.58

Thus,

`n= ((2.58*√(0.68(1-0.68)))/(0.05) )^2 \\ = ((2.58* √(0.2176) )/(0.05))^2= ((2.58(0.466476))/(0.05))^2 \\ = ((1.20351)/(0.05) )^2=(24.0702)^2=580`
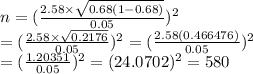
i.e. N ≥ 335.