Question

What is the true solution to the equation below 2 log3(6x)-log3(4x)=2 log 3(x+2)

A. x=-2 and x=1
B. x= -2 and x=2
C. x=1 and x=4
D. x=2 and x=4
It's C

Answer 1

C: x=1 and x=4

Explanation:

On edg

Answer 2

Answer: The answer is (C) C. x=1 and x=4.

Step-by-step explanation: We are given to find the true solution of the following equation involving logarithms:

`2\log_36x-\log_34x=2\log_3(x+2).`

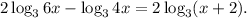
We will be using the following properties of logarithms in the solution.

`(i)~a\log b=\log a^b,\\\\(ii)~\log a-\log b=\log(a)/(b).`

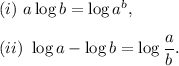
The solution is as follows:

`2\log_36x-\log_34x=2\log_3(x+2)\\\\\Rightarrow \log_3(6x)^2-\log_34x=\log_3(x+2)^2\\\\\\\Rightarrow \log_3(36x^2)/(4x)=\log_3(x^2+4x+4)\\\\\\\Rightarrow 9x=x^2+4x+4\\\\\Rightarrow x^2-5x+4=0\\\\\Rightarrow (x-4)(x-1)=0\\\\\Rightarrow x-4=0,~~~x-1=0\\\\\Rightarrow x=4,~~~x=1.`

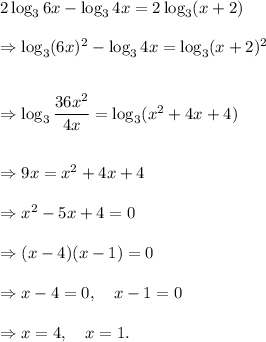
Since we can find the logarithm of a positive integer only, and both the solutions x = 1 and 4 satisfy this condition after substituting in the given equation, so both the solutions are TRUE.

Thus, the correct option is (C).