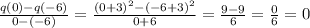Question

Match each interval with its corresponding average rate of change for q(x) = (x + 3)2. 1. -6 ≤ x ≤ -4 1 2. -3 ≤ x ≤ 0 -4 3. -6 ≤ x ≤ -3 0 4. -3 ≤ x ≤ -2 -1 5. -4 ≤ x ≤ -3 3 6. -6 ≤ x ≤ 0 -3

Answer 1

The average rate of change of a function f(x) in an interval, a < x < b is given by

`(f(b) - f(a))/(b - a)`

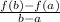
Given q(x) = (x + 3)^2

1.) The average rate of change of q(x) in the interval -6 ≤ x ≤ -4 is given by
`(q(-4)-q(-6))/(-4-(-6)) = ((-4+3)^2-(-6+3)^2)/(-4+6) = (1-9)/(2) = (-8)/(2) =-4`

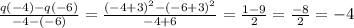
2.) The average rate of change of q(x) in the interval -3 ≤ x ≤ 0 is given by
`(q(0)-q(-3))/(0-(-3)) = ((0+3)^2-(-3+3)^2)/(0+3) = (9-0)/(3) = (9)/(3) =3`

3.) The average rate of change of q(x) in the interval -6 ≤ x ≤ -3 is given by
`(q(-3)-q(-6))/(-3-(-6)) = ((-3+3)^2-(-6+3)^2)/(-3+6) = (0-9)/(3) = (-9)/(3) =-3`

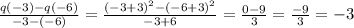
4.) The average rate of change of q(x) in the interval -3 ≤ x ≤ -2 is given by
`(q(-2)-q(-3))/(-2-(-3)) = ((-2+3)^2-(-3+3)^2)/(-2+3) = (1-0)/(1) = (1)/(1) =1`

5.) The average rate of change of q(x) in the interval -4 ≤ x ≤ -3 is given by
`(q(-3)-q(-4))/(-3-(-4)) = ((-3+3)^2-(-4+3)^2)/(-3+4) = (0-1)/(1) = (-1)/(1) =-1`

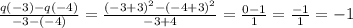
6.) The average rate of change of q(x) in the interval -6 ≤ x ≤ 0 is given by
`(q(0)-q(-6))/(0-(-6)) = ((0+3)^2-(-6+3)^2)/(0+6) = (9-9)/(6) = (0)/(6) =0`