Given
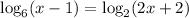
I attached a graphical solution to the equation. The blue curve represent
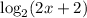
while the red curve represent
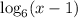
From the equation, it can be seen that the curves representing the two terms in both sides of the equation does not meet.
Therefore, the statement about the graph that is true is "The curves do not intersect".