Answer: D.
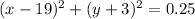
Explanation:
Let's review what we know:
- the lake is circular
- the town hall is at the origin
- the center of the lake is 19 miles east of the origin and
- 3 miles south of it
- the radius of the lake is 0.5 miles
A circle can be depicted on the coordinate plane with the equation
 , where:
, where:
- (h, k) is the center of the circle
- and r is the radius of the circle
19 miles east of the origin would be 19 units to the right of the origin on the coordinate plane, as east is the rightwards direction in real life. In short, h = 19.
Let's plug in that value:
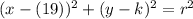 .
.
So we know that the x-coordinate defining part of the equation would have to be
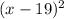 .
.
Meanwhile, 3 miles south of the origin would be modeled as three units underneath it, because south would be considered "downwards". The y-value (k) would be negative 3.
Putting what we have so far together, the center of the circle would be (19, -3).
Therefore, the y-coordinate defining part of the equation would be
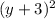 .
.
Here's what the equation looks like with the work we've completed so far:
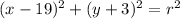
Finally, let's plug in the radius value 0.5.
0.5 * 0.5 = 0.25
Ailani would use the equation
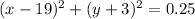 to model the lake in relation to the town hall. I hope that makes sense!
to model the lake in relation to the town hall. I hope that makes sense!