Question

How ?

integral sinx / 4 + sinx dx

Answer 1

The standard approach is to employ the substitution
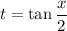
`t=\tan\frac x2`. Then
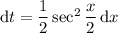
`\mathrm dt=\frac12\sec^2\frac x2\,\mathrm dx`. You can derive the following relations:


`\tan\frac x2=t\iff(\sin\frac x2)/(\cos\frac x2)=\frac{\frac t{√(1+t^2)}}{\frac1{√(1+t^2)}}`

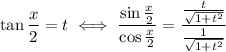
(where the choice of
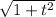
`√(1+t^2)` comes from the fact that it satisfies the Pythagorean theorem,
`1^2+t^2=(√(1+t^2))^2=1+t^2`)


`\sin x=\sin\frac{2x}2=2\sin\frac x2\cos\frac x2=2\frac t{√(1+t^2)}\frac1{√(1+t^2)}=(2t)/(1+t^2)`

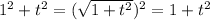
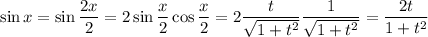
and we also have


`\mathrm dt=\frac12\sec^2\frac x2\,\mathrm dx\implies2\cos^2\frac x2\,\mathrm dt=\mathrm dx\implies\mathrm dx=\frac2{1+t^2}\,\mathrm dt`

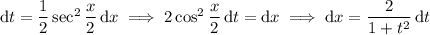
So the integral can be written as


`\displaystyle\int(\sin x)/(4+\sin x)\,\mathrm dx=\int((2t)/(1+t^2))/(4+(2t)/(1+t^2))\frac2{1+t^2}\,\mathrm dt`

Simplifying the integrand gives


`\displaystyle2\int\frac t{(2t^2+t+2)(t^2+1)}\,\mathrm dt`

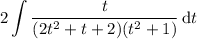
which can be expanded into partial fractions, yielding


`\displaystyle2\int\left(\frac1{t^2+1}-\frac2{2t^2+t+2}\right)\,\mathrm dt`

The first integral can be handled immediately (
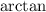
`\arctan`), while the other needs rewriting in order to be computed similarly. Complete the square in the denominator to get


`2t^2+t+2=2\left(t+\frac14\right)^2+\frac{15}8`

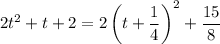
and cancelling a factor of 2, you'll end up with


`\displaystyle2\int\left(\frac1{t^2+1}-\frac1{\left(t+\frac14\right)^2+(15)/(16)}\right)\,\mathrm dt`

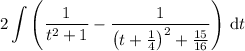
Proper trigonometric substitutions will complete the work. (And of course you'll need to back-substitute to get the result in terms of
`x`.)