Question

Find a negative real number such that the square of the sum of a number and 5 is equal to 48

Answer 1

Let x = negative real number ⇒x<0

from the statement above, we can generate an equation:
(x + 5)² = 48

`\sqrt{(x+5)^(2) }`=
`√(48)`
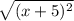
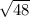
⇒ eliminate the square by getting the square root on both sides


`√(48) = \left \{ {{=4 √(3) } \atop {=-4 √(3) }} \right.`
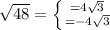
⇒ the perfect square of a real number has one positive real number and a negative real number

transposing 5 to other side, we will arrive at two (2) values for x:


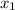
`x_(1)` = -5 - 4√3 = -11.928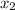

`x_(2)` = -5 + 4√3 = 1.928

Since we are only looking at the negative real number, our answer will be -11.928, also equal to -5 - 4√3.