Answer:
The graph of f(x) vertically stretch by factor 2.
Explanation:
The given functions are
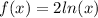

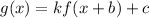
Where, k is stretch factor, b is horizontal shift and c is vertical shift.
If k>1, then it represents vertical stretch and if k<1, then it represents vertical compression.
If b>0, then the graph of f(x) shifts b units left and if b<0, then the graph of f(x) shifts b units right.
If c>0, then the graph of f(x) shifts c units up and if c<0, then the graph of f(x) shifts c units down.
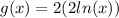
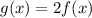
The stretch factor is 2>0, it means the graph of f(x) vertically stretch by factor 2.