Question

Each pound of food C contains 6 ounces of ingredient P and 3 ounces of ingredient Q. Each pound of food D contains 4.5 ounces of ingredient P and 1.5 ounces of ingredient Q. How much food C and how much food D are needed to obtain a mixture containing 144 ounces of P and 60 ounces of Q?

Answer 1

so hmm the food C = 6p + 3q and the food D = 4.5p + 1.5q

now, if we check how much is the ratios of C/D for each component, then, mixture M = 144p + 60q, must contain the same ratio for each "p" and "q" component


`\bf \textit{ratio of`

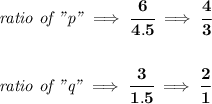
so, if we divide the 144p by 4+3, or 7 even pieces, 4 must belong to food C and 3 to food D, retaining the ratio of 4/3

and we do the same for 60q, we divide it in 2+1 or 3 even pieces, but that one is very clear, 2 must belong to food C and 1 to food D, 60/3 is clear ends up with a ratio of 40 and 20

now the "p" part... ends up as
`\bf \cfrac{144}{7}\cdot 4\qquad and\qquad \cfrac{144}{7}\cdot 3\implies \cfrac{576}{7}\qquad and\qquad \cfrac{432}{7}`

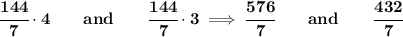
that's what I see it, as the ratio of 4/3 and 2/1 being retained in the mixture M