Question

Pipe 1 can fill a reservior in 45 hours. Pipes 1 and 2 together can fill it in 30 hours. Pipes 2 and 3 together can fill it in 40 hours, In how much time can Pipe 2 alone and in how much time can Pipe 3 alone fill the reservior?

Answer 1

now let's say hmmm
p1 = pipe1 p2 = pipe2 and p3 = pipe3

so, we know p1 can do the whole shebang in 45hours
that simply means, that in 1hr, percentage wise, p1 can do really (1/45)th of the job

ok... now, if we have p1 and p2 working together, they can do the whole thing in 30hrs, so, in 1hr, they both working, have done only (1/30)th of the job, so, what's p2's rate? well


`\bf \begin{array}{clclclll} \cfrac{1}{45}&+&\cfrac{1}{p2}&=&\cfrac{1}{30}\\ \uparrow &&\uparrow &&\uparrow \\ \textit{p1's rate/hr}&&\textit{p2's rate/hr}&&\textit{both's rate/hr} \end{array}\\\\ -----------------------------\\\\ \cfrac{1}{p2}=\cfrac{1}{30}-\cfrac{1}{45}\implies \cfrac{1}{p2}=\cfrac{1}{90}\implies \boxed{90=p2}`

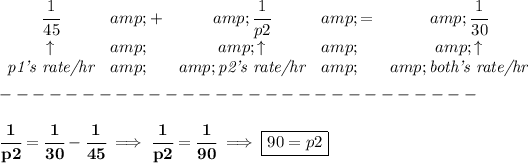
that simply means, p2 can do the whole job in 90 hours... notice, 90 is 45*2, that just means p2 is twice as slow as p1

now.. we know p2 and p3 working together can do the job in 40hrs, what's p3's rate?

well
`\bf \begin{array}{clclclll} \cfrac{1}{p3}&+&\cfrac{1}{90}&=&\cfrac{1}{40}\\ \uparrow &&\uparrow &&\uparrow \\ \textit{p3's rate/hr}&&\textit{p2's rate/hr}&&\textit{both's rate/hr} \end{array}\\\\ -----------------------------\\\\ \cfrac{1}{p3}=\cfrac{1}{40}-\cfrac{1}{90}\implies \cfrac{1}{p3}=\cfrac{1}{72}\implies \boxed{72=p3}`

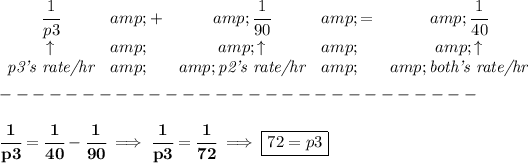
so p3, can do the whole shebang in 72hrs then