Question

A kite with a 100 foot-long string is caught in a tree. When the full length of the string is stretched in a straight line to the ground, it touches the ground a distance of 30 feet from the bottom of the tree. Find the measure of the angle between the kite string and the ground.

Answer 1

hyp=100,adj side=30

angle=
`cos^(-1)(30/100)`

Answer 2

The measure of the angle between the kite string and the ground is 72.54°.

Explanation:

Given : A kite with a 100 foot-long string is caught in a tree. When the full length of the string is stretched in a straight line to the ground, it touches the ground a distance of 30 feet from the bottom of the tree.

To find : The measure of the angle between the kite string and the ground.

Solution :

Refer the attached figure.

In a right angle ΔABC,

A kite with a 100 foot-long string is caught in a tree.

i.e, AC=100 ft.

Length of the string touches the ground a distance of 30 feet from the bottom of the tree.

i.e, BC=30 ft.

We have to find the angle C between the kite string and the ground.

Apply trigonometric function,

`\cos\theta=\frac{\text{Base}}{\text{Hypotenuse}}`

`\cos\theta=\frac{\text{BC}}{\text{AC}}`

`\cos\theta=(30)/(100)`

`\cos\theta=0.3`

`\theta=\cos^(-1)(0.3)`

`\theta=72.54^\circ`

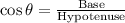
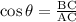
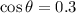
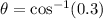
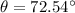
Therefore, The measure of the angle between the kite string and the ground is 72.54°.