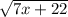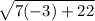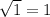First of all, you have to understand
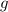 is a square-root function.
is a square-root function.
Square-root functions are continuous across their entire domain, and their domain is all real x-values for which the expression within the square-root is non-negative.
In other words, for any square-root function
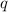 and any input
and any input
 in the domain of
in the domain of
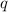 (except for its endpoint), we know that this equality holds:
(except for its endpoint), we know that this equality holds:
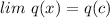
Let's take
 as an example.
as an example.
The domain of
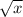 is all real numbers such that
is all real numbers such that
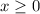 . Since
. Since
 is the endpoint of the domain, the two-sided limit at that point doesn't exist (you can't approach
is the endpoint of the domain, the two-sided limit at that point doesn't exist (you can't approach
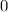 from the left).
from the left).
However, continuity at an endpoint only demands that the one-sided limit is equal to the function's value:

In conclusion, the equality
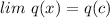 holds for any square-root function
holds for any square-root function
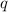 and any real number
and any real number
 in the domain of
in the domain of
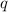 except for its endpoint, where the two-sided limit should be replaced with a one-sided limit.
except for its endpoint, where the two-sided limit should be replaced with a one-sided limit.
The input
 , is within the domain of
, is within the domain of
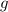 .
.
Therefore, in order to find
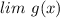 we can simply evaluate
we can simply evaluate
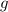 at
at
 .
.