Instantaneous rate of change can be found by finding the derivative of the equation.
a) Given the function
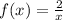
The equation in this particular problem can be rewritten as follows:
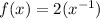
The derivate is
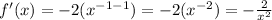
From here we can plug in our given, x=2, and get the answer
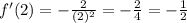
Answer: -1/2
b) The function

Applying the power rule for derivatives
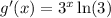
And we can plug in our given, x=2, and get the answer
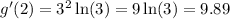
Answer: 9.89