Question

Prove that


`\mathsf=\sum_(k=1)^n k.`

for all natural n.

=====

Take this seriously. Jokes and spam will be reported right away.

Answer 1

Let's start from what we know.


`(1)\qquad\sum\limits_(k=1)^n1=\underbrace{1+1+\ldots+1}_(n)=n\cdot 1=n\\\\\\ (2)\qquad\sum\limits_(k=1)^nk=1+2+3+\ldots+n=(n(n+1))/(2)\quad\text{(arithmetic series)}\\\\\\ (3)\qquad\sum\limits_(k=1)^nk\ \textgreater \ 0\quad\implies\quad\left|\sum\limits_(k=1)^nk\right|=\sum\limits_(k=1)^nk`

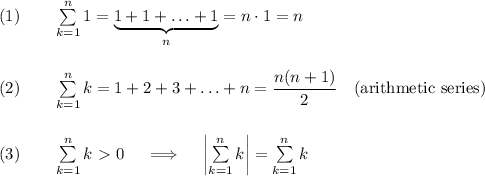
Note that:


`\sum\limits_(k=1)^n(-1)^k\cdot k^2=(-1)^1\cdot1^2+(-1)^2\cdot2^2+(-1)^3\cdot3^2+\dots+(-1)^n\cdot n^2=\\\\\\=-1^2+2^2-3^2+4^2-5^2+\dots\pm n^2`

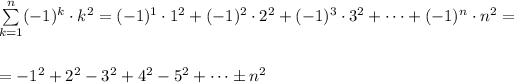
(sign of last term will be + when n is even and - when n is odd).
Sum is finite so we can split it into two sums, first
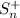
`S_n^+` with only positive trems (squares of even numbers) and second
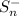
`S_n^-` with negative (squares of odd numbers). So:


`\sum\limits_(k=1)^n(-1)^k\cdot k^2=S_n^+-S_n^-`

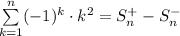
And now the proof.

1) n is even.

In this case, both
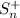
`S_n^+` and
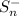
`S_n^-` have
`(n)/(2)` terms. For example if n=8 then:


`S_8^+=\underbrace{2^2+4^2+6^2+8^2}_{(8)/(2)=4}\qquad\text{(even numbers)}\\\\\\ S_8^-=\underbrace{1^2+3^2+5^2+7^2}_{(8)/(2)=4}\qquad\text{(odd numbers)}\\\\\\`

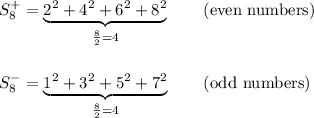
Generally, there will be:


`S_n^+=\sum\limits_(k=1)^(n)/(2)(2k)^2\\\\\\S_n^-=\sum\limits_(k=1)^(n)/(2)(2k-1)^2\\\\\\`

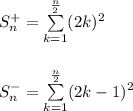
Now, calculate our sum:


`\left|\sum\limits_(k=1)^n(-1)^k\cdot k^2\right|=\left|S_n^+-S_n^-\right|= \left|\sum\limits_(k=1)^(n)/(2)(2k)^2-\sum\limits_(k=1)^(n)/(2)(2k-1)^2\right|=\\\\\\= \left|\sum\limits_(k=1)^(n)/(2)4k^2-\sum\limits_(k=1)^(n)/(2)\left(4k^2-4k+1\right)\right|=\\\\\\`


`=\left|4\sum\limits_(k=1)^(n)/(2)k^2-4\sum\limits_(k=1)^(n)/(2)k^2+4\sum\limits_(k=1)^(n)/(2)k-\sum\limits_(k=1)^(n)/(2)1\right|=\left|4\sum\limits_(k=1)^(n)/(2)k-\sum\limits_(k=1)^(n)/(2)1\right|\stackrel{(1),(2)}{=}\\\\\\= \left|4((n)/(2)((n)/(2)+1))/(2)-(n)/(2)\right|=\left|2\cdot(n)/(2)\left((n)/(2)+1\right)-(n)/(2)\right|=\left|n\left((n)/(2)+1\right)-(n)/(2)\right|=\\\\\\`


`=\left|(n^2)/(2)+n-(n)/(2)\right|=\left|(n^2)/(2)+(n)/(2)\right|=\left|(n^2+n)/(2)\right|=\left|(n(n+1))/(2)\right|\stackrel{(2)}{=}\\\\\\\stackrel{(2)}{=} \left|\sum\limits_(k=1)^nk\right|\stackrel{(3)}{=}\sum\limits_(k=1)^nk`

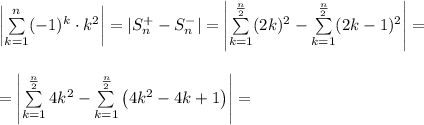
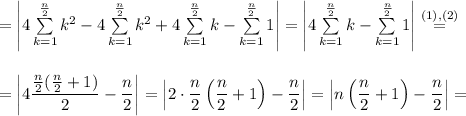
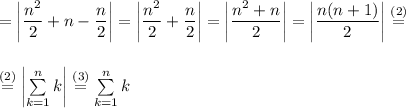
So in this case we prove, that:


`\left|\sum\limits_(k=1)^n(-1)^k\cdot k^2\right|=\sum\limits_(k=1)^nk`

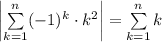
2) n is odd.

Here,
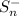
`S_n^-` has more terms than
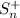
`S_n^+`. For example if n=7 then:


`S_7^-=\underbrace{1^2+3^2+5^2+7^2}_{(n+1)/(2)=(7+1)/(2)=4}\\\\\\ S_7^+=\underbrace{2^2+4^4+6^2}_{(n+1)/(2)-1=(7+1)/(2)-1=3}\\\\\\`

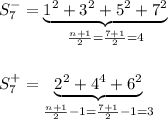
So there is
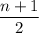
`(n+1)/(2)` terms in
`S_n^-`,
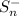
`(n+1)/(2)-1` terms in
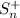
`S_n^+` and:


`S_n^+=\sum\limits_(k=1)^{(n+1)/(2)-1}(2k)^2\\\\\\ S_n^-=\sum\limits_(k=1)^{(n+1)/(2)}(2k-1)^2`

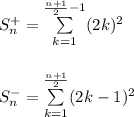
Now, we can calculate our sum:


`\left|\sum\limits_(k=1)^n(-1)^k\cdot k^2\right|=\left|S_n^+-S_n^-\right|= \left|\sum\limits_(k=1)^{(n+1)/(2)-1}(2k)^2-\sum\limits_(k=1)^{(n+1)/(2)}(2k-1)^2\right|=\\\\\\= \left|\sum\limits_(k=1)^{(n+1)/(2)-1}4k^2-\sum\limits_(k=1)^{(n+1)/(2)}\left(4k^2-4k+1\right)\right|=\\\\\\= \left|\sum\limits_(k=1)^{(n-1)/(2)-1}4k^2-\sum\limits_(k=1)^{(n+1)/(2)}4k^2+\sum\limits_(k=1)^{(n+1)/(2)}4k-\sum\limits_(k=1)^{(n+1)/(2)}1\right|=\\\\\\`


`=\left|\sum\limits_(k=1)^{(n-1)/(2)-1}4k^2-\sum\limits_(k=1)^{(n+1)/(2)-1}4k^2-4\left((n+1)/(2)\right)^2+\sum\limits_(k=1)^{(n+1)/(2)}4k-\sum\limits_(k=1)^{(n+1)/(2)}1\right|=\\\\\\= \left|-4\left((n+1)/(2)\right)^2+4\sum\limits_(k=1)^{(n+1)/(2)}k-\sum\limits_(k=1)^{(n+1)/(2)}1\right|\stackrel{(1),(2)}{=}\\\\\\ \stackrel{(1),(2)}{=}\left|-4(n^2+2n+1)/(4)+4((n+1)/(2)\left((n+1)/(2)+1\right))/(2)-(n+1)/(2)\right|=\\\\\\`


`=\left|-n^2-2n-1+2\cdot(n+1)/(2)\left((n+1)/(2)+1\right)-(n+1)/(2)\right|=\\\\\\= \left|-n^2-2n-1+(n+1)\left((n+1)/(2)+1\right)-(n+1)/(2)\right|=\\\\\\= \left|-n^2-2n-1+((n+1)^2)/(2)+n+1-(n+1)/(2)\right|=\\\\\\= \left|-n^2-n+(n^2+2n+1)/(2)-(n+1)/(2)\right|=\\\\\\= \left|-n^2-n+(n^2)/(2)+n+(1)/(2)-(n)/(2)-(1)/(2)\right|=\left|-(n^2)/(2)-(n)/(2)\right|=\left|-(n^2+n)/(2)\right|=\\\\\\`


`=\left|-(n(n+1))/(2)\right|=|-1|\cdot\left|(n(n+1))/(2)\right|=\left|(n(n+1))/(2)\right|\stackrel{(2)}{=}\left|\sum\limits_(k=1)^nk\right|\stackrel{(3)}{=}\sum\limits_(k=1)^nk`

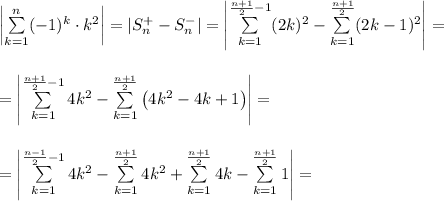
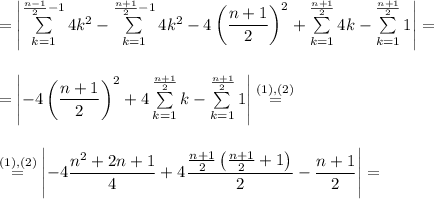
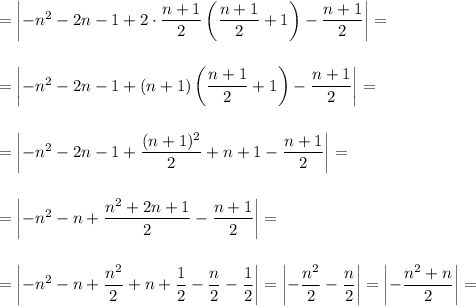
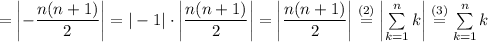
We consider all possible n so we prove that:


`\forall_{n\in\mathbb{N}}\quad\left|\sum\limits_(k=1)^n(-1)^k\cdot k^2\right|=\sum\limits_(k=1)^nk`