Question

Consider the following geometric sequence. -5,10,-20,40... If the explicit formula for the sequence above is expressed...

Answer 1

To fit the formula, b is the first term, -5, and c is the common ratio, or -2

Answer 2

The explicit formula for the geometric sequence is given by:

`a_n = a_1 \cdot r^(n-1)`

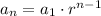
where,

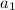`a_1` si the first term

r is the common ratio of the terms.

As per the statement:

Consider the following geometric sequence. -5, 10, -20, 40...

First term(
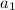`a_1`) = -5

Common ratio(r) = -2

Since,

`(10)/(-5) = -2`,

`(-20)/(10) = -2`,

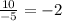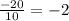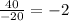`(40)/(-20) = -2` and so on...

Substitute the given values in [1] we have;

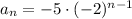`a_n = -5 \cdot (-2)^(n-1)` where, n is the number of term.

On comparing the equation
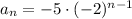`a_n = -5 \cdot (-2)^(n-1)` with
`a_n = b \cdot c^(n-1)` we get;

b = -5 and c = -2

Therefore, the values of b and c are:

b = -5 and c = -2