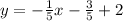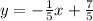Question

The equation of line LM is y = 5x + 4. Write an equation of a line perpendicular to line LM in slope-intercept form that contains point (−3, 2).

Answer 1

Hello:
the equation is : y = ax+b
the slope is a : a×(5) = -1......( perpendicular to a line with a slope of 5)

a = -1/5 y=(-1/5)x+b
the line that passes through (-3, 2) 2 = (-1/5)(-3)+b
b =7/5
the equation is : y = (-1/5)x+7/5

Answer 2

`y=-(1)/(5)x+(7)/(5)`

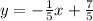
Explanation:

Line LM
`y=5x+4`

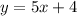
Find the equation of the line in slope intercept form perpendicular to LM

In y=mx+b , the slope is m

Line LM
`y=5x+4`

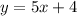
Slope of the given line is 5.

Slope of the perpendicular line is the negative reciprocal of the slope of the given line

Slope of the perpendicular line is
`-(1)/(5)`

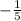
Use point slope form

`y-y_1=m(x-x_1)`

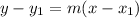
(x1,y1) is (-3,2)

`y-2=-(1)/(5)(x-(-3))`

`y-2=-(1)/(5)(x+3)`

`y-2=-(1)/(5)x-(3)/(5)`

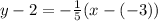
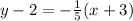
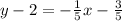
Add 2 on both sides

`y=-(1)/(5)x-(3)/(5)+2`

`y=-(1)/(5)x+(7)/(5)`