Answer:
CosP +CosQ =
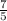 .
.
Explanation:
Given : In ΔPQR, ∠P and ∠Q are complimentary angles. If sinQ = 4/5 .
To find : cosP + cosQ =
Solution : We have given that ∠P and ∠Q are complimentary angles.
P + Q = 90 .
Q = 90 - P.
Then sin( 90 -p ) =
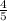 .
.
As we know that sin( 90 -p ) = CosP =
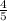 .
.
We have SinQ =
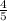 .
.
CosQ =
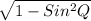
Plugging the value of SinQ
CosQ =
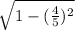 .
.
CosQ =
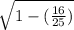 .
.
CosQ =
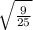 .
.
CosQ =
 .
.
CosP +CosQ =
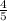 +
+
 .
.
CosP +CosQ =
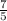 .
.
Therefore, CosP +CosQ =
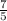 .
.