Question

Tom is using logarithms to solve the equation 3^2x = 32. Which of the following equations would be equivalent to his original expression?

2x log 3 =log 32
3 log 2x =32
2 log 3 = x log 32
x log 3 =2 log 32

Answer 1

3^(2x)=32 so taking log of both sides

2x*log3=log32

Answer 2

ANSWER


`2x \: log(3) = log(32)`

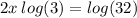
Step-by-step explanation

The given exponential equation is


`{3}^(2x) = 32`

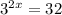
Tom is using logarithm to solve this question. Tom is expected to take logarithm of both sides of the exponential equation to a common base.

Let us say Tom took logarithm of both sides to base 10.

Then the equation becomes,


`log( {3}^(2x) ) = log(32)`

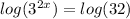
Tom needs to apply the following properties of logarithm :


`log( {a}^(n) ) =n \: log(a)`

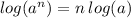
to the left hand side to obtain,


`2x \: log(3) = log(32)`

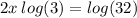
The correct answer is A.