Question

This figure is dilated by a factor of 1 2 , with the origin as center. Which statement is NOT correct? A) R(2, 8) → R'(1, 4) B) Q(10, 2) → Q'(5, 2) C) P(2, -4) → P'(1, -2) D) S(-10, 2) → S'(-5, 1)

Answer 1

Statement B would be the correct answer because the y's stayed the same. Having a dilation of 1/2 means that both the x and y from the original point will be multiplied by 1/2. Every other answer is multiplied by 1/2, meaning B is the correct answer.

Hope this helps! If you need further assistance or explanation, message me or comment under this post!

Answer 2

Option B.

Explanation:

If a figure is dilated by a factor of k , with the origin as center, then the rule of dilation is

`(x,y)\rightarrow (kx,ky)`

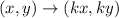
It is given that the given figure is dilated by a factor of 1 2 , with the origin as center. So, the rule of dilation is

`(x,y)\rightarrow ((1)/(2)x,(1)/(2)y)`

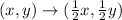
The vertices of image are

`R(2,8)\rightarrow R'(1,4)`

`Q(10,2)\rightarrow Q'(5,1)`

`P(2,-4)\rightarrow P'(1,-2)`

`S(-10,2)\rightarrow S'(-5,1)`

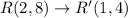
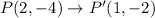
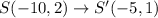
All the given statements are correct except Q(10, 2) → Q'(5, 2).

Therefore correct option is B.