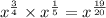Question

Multiply x to the 3 fourths power times x to the 1 fifth power

Answer 1

That would be x ^19/20 or if needed in radical form: 20 squareroot x^19. Hope this helped

Answer 2

`x^{(3)/(4)}* x^{(1)/(5)}=x^{(19)/(20)`

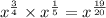
Explanation:

Given : Expression x to the 3 fourths power times x to the 1 fifth power

To find : Multiply the expression?

Solution :

Step 1 - Write the expression in number form,

`x^{(3)/(4)}* x^{(1)/(5)}`

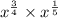
Step 2 - If base are same then in multiply power get add,

`=x^{(3)/(4)+(1)/(5)}`

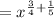
Step 3 - Add in power,

`=x^{(15+4)/(20)`

`=x^{(19)/(20)`

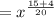
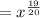
Therefore,
`x^{(3)/(4)}* x^{(1)/(5)}=x^{(19)/(20)`