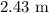Question

Two speakers are against a wall emitting a sound at 647 Hz, 5 m apart, and facing each other. You are standing against the wall in between the speakers. Use 344 m/s for the speed of sound in air.A) What is the closest distance that you can be from the speaker on the left at which you experience total destructive interference, and the sound from the speakers cancel out? Round your answer to 2 decimal places.B) What is the closest distance that you can be from the speaker on the left at which you experience total constructive interference, and the sound intensity is doubled? Round your answer to 2 decimal places.

Answer 1

Given Data:

*The frequency of the sound is:

`\begin{gathered} f=647\text{ Hz} \\ =647\text{ s}^(-1) \end{gathered}`

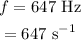
*The speed of sound in air is:

`v=344\text{ m/s}`

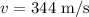
*The distance between the speakers is:

`d=5\text{ m}`

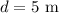
Step-by-step explanation:

The wavelength of the sound is given by:

`\begin{gathered} \lambda=(v)/(f) \\ =\frac{344\text{ m/s}}{647\text{ s}^(-1)} \\ =0.532\text{ m} \end{gathered}`

Let us consider that we are standing at point P in the figure below.

The path difference will be:

`\begin{gathered} \Delta x=(5-x)-x \\ =5-2x \end{gathered}`

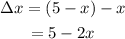
A)

For destructive interference:

`\begin{gathered} \Delta x=(\lambda)/(2) \\ 5-2x=\frac{0.532\text{ m}}{2} \\ 5-2x=0.266\text{ m} \\ 5-0.266\text{ m = }2x \\ (4.734m)/(2)=x \\ x=2.37\text{ m} \end{gathered}`

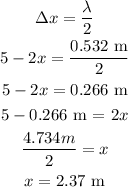
B)

When the intensity doubles, the frequency also doubles. So, the wavelength will be:

`\begin{gathered} \lambda^(\prime)=(v)/(2f) \\ =(\lambda)/(2) \end{gathered}`

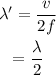
For constructive interference, path difference is:

`\begin{gathered} \Delta x=(\lambda^(\prime))/(2) \\ 5-2x=(\lambda)/(4) \\ 5-2x=\frac{0.532\text{ m}}{4} \\ 5-2x=0.133\text{ m} \\ 5-0.133\text{ m}=2x \\ (4.867m)/(2)=x \\ x=2.43\text{ m} \end{gathered}`

Final Answer:

A) The closest distance will be:

`2.37\text{ m}`

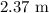
B) The closest distance will be:

`2.43\text{ m}`