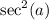Question

Compute the limit:

lim (tan x – tan a)/tan(x – a)
x → a

without L'Hospital's Rule.

=====

Take this seriously. Jokes and spam will be reported right away.

Answer 1

So you can actually use a couple trig identities
tan(x-a) =(tan x-tan a)/(1+tan x*tan a)
From there, easy!
(tan x-tan a)/(tan x-tan a)/(1+tan x*tan a)
1/1/(1+tan x*tan a)
which is
(1+tanx*tana)
1+tan^2a
sec^2 a
typo, forgot the 1/1

Answer 2

`\displaystyle \sec ^(2) (a)`

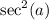
Explanation:

we are given a limit

`\displaystyle \lim_(x \to a) ( \tan(x) - \tan(a) )/( \tan(x - a) )`

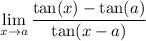
and said to compute without L'Hopitâl rule

if we substitute a for x directly we'd get

`\displaystyle ( \tan(a) - \tan(a) )/( \tan(a - a) )`

`\displaystyle \: (0)/(0)`

which is indeterminate

so we have to do it differently

recall trigonometric indentity

`\sf \displaystyle \tan(A\pm B)=(\tan(A)\pm \tan(B))/(1\mp \tan(A)\tan(B))`

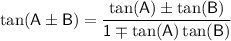
using the identity we get

`\displaystyle \lim_(x \to a) ( \tan(x) - \tan(a) )/( (\tan(x) - \tan(a))/(1 + \tan(x)\tan(a)))`

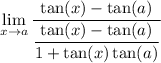
simplify complex fraction:

`\sf \displaystyle \lim_(x \to a) \cancel{\tan(x) - \tan(a)} * \frac{1 + \tan(x) \tan(a) }{ \cancel{\tan(x) - \tan(a) } }`

`\displaystyle \lim_(x \to a) 1 + \tan(x) \tan(a)`

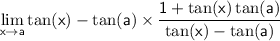
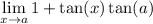
now we can substitute a for x:

`\displaystyle 1 + \tan(a) \tan(a)`

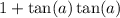
simplify multiplication:

`\displaystyle 1 + \tan ^(2) (a)`

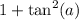
recall trigonometric indentity:

`\displaystyle \sec ^(2) (a)`