Question

An average adult has a total lung capacity of 6.0 L. How many total grams of air could be held in the lungs at a pressure of 102 kPa and a normal body temperature of 37° Celsius? (Assume that the average molar mass of air is 29 g/mol.)

Answer 1

You're able to figure this out by using the ideal gas equation PV=nRT Where R=.08 (L*atm/mol*K) Convert 37 C to Kelvin=310 K and 102 kPa to atm=roughly 1 atm Manipulate the ideal gas equation to n=PV/RT Plug in your values (1 atm * 6 L) / (.08 (L*atm/mol*K) * 310 K) All units should cancel except for mol and you should get .24 mol. Multiply the molar mass of air by your answer. .24 mol * 29 g/mol moles should cancel and you should get 6.9 g.

Answer 2

Answer: The amount of air that could be held in lungs is 6.873g

Step-by-step explanation:

To calculate the amount of air, we use the equation given by Ideal gas equation, which follows:

`PV=nRT`

where,

P = Pressure of the gas = 102 kPa

V = volume of the gas = 6 L

n = number of moles of gas = ? mol

R = Gas constant =
`8.31\text{L kPa }mol^(-1)K^(-1)`

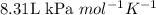
T = temperature of the gas = 37°C = 310 K (Conversion factor:
`T(K)=T(^oC)+273)`

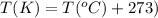
Putting values in above equation, we get:

`102kPa* 6L=n* 8.31\text{L kPa }* 310K\\\\n=0.237mol`

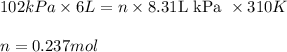
To calcultae the mass of the air, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

We are given:

Moles of air entered = 0.237 mol

Molar mass of air = 29 g/mol

Putting values in above equation, we get:

`0.237mol=\frac{\text{Mass of air}}{29g/mol}\\\\\text{Mass of air}=6.873g`

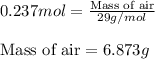
Hence, the amount of air that could be held in lungs is 6.873g