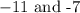Question

Solve.One number is 4 less than a second number. Twice the second number is 30 more than 4 times the first. Find the two numbers.

Answer 1

From the information available;

Let the numbers be x and y.

One number is 4 less than a second number. This would be tranlated as x is 4 less than y, or;

`x=y-4`

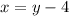
Also, twice the second number is 30 more than 4 times the first, that is

`\begin{gathered} 2* y=30+(4* x) \\ OR \\ 2y=30+4x \end{gathered}`

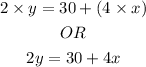
We now have a system of simultaneous equations which we shall solve as follows;

`\begin{gathered} x=y-4---(1) \\ 2y=30+4x---(2) \\ \text{Substitute for x=y-4 into equation (2)} \\ 2y=30+4(y-4) \\ 2y=30+4y-16 \\ \text{Collect all like terms;} \\ 2y-4y=30-16 \\ -2y=14 \\ \text{Divide both sides by -2;} \\ -(2y)/(-2)=(14)/(-2) \\ y=-7 \\ \text{Substitute for the value of y into equation (1)} \\ x=y-4 \\ x=-7-4 \\ x=-11 \end{gathered}`

ANSWER:

The two numbers are;

`-11\text{ and -7}`