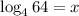Question

Express 64 = 4x as a logarithmic equation

A. log(4)X=64
B. log(4)64=x
C. log(64)4=x
D. log(64)X=4

Answer 1

Note: I'm assuming you mean that
`64=4^x`.

Taking the logarithm gives:


`\log{4^x} = \log{64}`

Using our rules of logarithms (
`\log{a^b} = b \log a`), we have:


`x \log 4 = \log 64`

This corresponds to answer A.

Answer 2

Option B is correct

`\log_4 64 = x`

Explanation:

using logarithmic rules:

`\log a^b = b\log a`

`\log_n m = (\log m)/(\log n)`

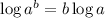
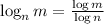
Given the equation:

`64 = 4^x`

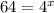
Take log both sides we have;

`\log 64 = \log 4^x`

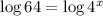
Apply the logarithmic rules:

`\log 64 = x\log 4`

Divide both sides by log 4 we have;

`(\log 64)/(\log 4)= x`

Again, apply the logarithmic rules:

`\log_4 64 = x`

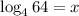
therefore, we get the given expression as a logarithmic equation is,
`\log_4 64 = x`