Question

Quadrilateral A’B’C’D’ is a dilation of quadrilateral ABCD about point P. Quadrilateral ABCD is shown. Side AB is labeled 5. Side BC is labeled 4. Side CD is labeled 10. Side DA is labeled 6. Quadrilateral A prime B prime C prime D prime is between quadrilateral ABCD and point P. Side A prime B prime is labeled 1 and one fourth. Side B prime C prime is labeled one. Side C prime D prime is labeled 2 and a half. Side D prime A prime is labeled 1 and a half. reduction enlargement

Answer 1

A reduction

Explanation:

Answer 2

Answer: The correct option is (A) reduction.

Step-by-step explanation: Given that the quadrilateral A'B'C'D' is a dilation of the quadrilateral ABCD.

As shown in the given figure, the lengths of the sides of quadrilateral ABCD are as follows:

AB = 5 units, BC = 4 units, CD = 10 units and DA = 6 units.

And, the lengths of the sides of quadrilateral A'B'C'D' are as follows:

`A'B'=1(1)/(4)=(5)/(4)~\textup{units},~~B'C'=1~\textup{units},~~C'D'=2(1)/(2)=(5)/(2)~\textup{units},\\\\D'A'=1(1)/(2)=(3)/(2)~\textup{units}.`

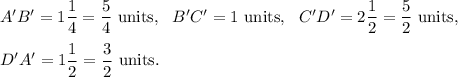
We know that the dilation will be an enlargement if the scale factor is greater than 1 and it will be a reduction if the scale factor is less than 1.

Now, the scale factor is given by

`S=\frac{\textup{length of a side of the dilated figure}}{\textup{length of the corresponding side of the original figure}}\\\\\\\Rightarrow S=(A'B')/(AB)=((5)/(4))/(5)=(5)/(4*5)=(1)/(4)<1.`

Since the scale factor is less than 1, so the dilation will be a reduction.