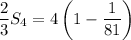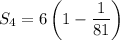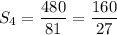It's evident that the first four terms are 4, 4/3, 4/9, and 4/27. So the fourth partial sum of the series is
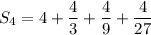
It's as easy as adding up the fractions, but I bet this is supposed to be an exercise in taking advantage of the fact that the series is geometric and use the well-known formula for computing such a sum.
Multiply the sum by 1/3 and you have
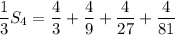
Now subtracting this from
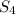
gives
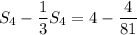
That is, all the matching terms will cancel. Now solving for
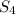
, you
have