Question

Determine whether the set of vectors
`v_{1=(3,2,1), v_(2) =(-1,-2,-4) and v_{3 =(1,1,-1)` will span R3?

Answer 1

Since each vector is a member of
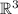
`\mathbb R^3`, the vectors will span
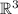
`\mathbb R^3` if they form a basis for
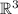
`\mathbb R^3`, which requires that they be linearly independent of one another.

To show this, you have to establish that the only linear combination of the three vectors
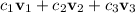
`c_1\mathbf v_1+c_2\mathbf v_2+c_3\mathbf v_3` that gives the zero vector
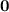
`\mathbf0` occurs for scalars
`c_1=c_2=c_3=0`.


`c_1\begin{bmatrix}3\\2\\1\end{bmatrix}+c_2\begin{bmatrix}-1\\-2\\-4\end{bmatrix}+c_3\begin{bmatrix}1\\1\\-1\end{bmatrix}=(0,0,0)\iff\begin{bmatrix}3&-1&1\\2&-2&1\\1&-4&-1\end{bmatrix}\begin{bmatrix}c_1\\c_2\\c_3\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix}`

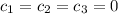
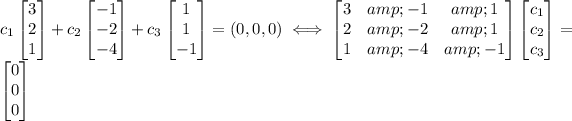
Solving this, you'll find that
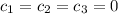
`c_1=c_2=c_3=0`, so the vectors are indeed linearly independent, thus forming a basis for
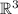
`\mathbb R^3` and therefore they must span
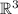
`\mathbb R^3`.