Answer:
The proportion
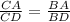 holds when AD is the bisector of ∠ A that is ∠BAD = ∠CAD
holds when AD is the bisector of ∠ A that is ∠BAD = ∠CAD
Explanation:
Given : Ellen has property whose boundary lines form a triangle. Her house lies at vertex A, and she is going to put a bunkhouse for the ranch hands somewhere along the segment BC.
She wants the placement to be such that
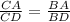
We have to find what must be true about the segment AD so that the proportion
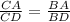 holds.
holds.
CONVERSE OF ANGLE BISECTOR THEOREM states that if a point D on the side BC of triangle ABC divides BC in the same ratio as the sides AB and AC, then AD is the angle bisector of angle ∠ A.
Thus, applying converse of angle bisector theorem,
The proportion
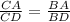 holds when AD is the bisector of ∠ A.
holds when AD is the bisector of ∠ A.
that is ∠BAD = ∠CAD
Thus, The proportion
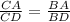 holds when AD is the bisector of ∠ A. that is ∠BAD = ∠CAD
holds when AD is the bisector of ∠ A. that is ∠BAD = ∠CAD