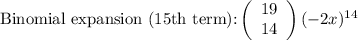Question

. Using the Binomial Theorem explicitly, give the 15th term in the expansion of (-2x + 1)^19

Answer 1

Let's rewrite the binomial as:

`(1 - 2x)^(19)`


`\text{Binomial expansion:} (1 + x)^(n) = \sum_(r = 0)^n\left(\begin{array}{ccc}n\\r\end{array}\right) (x)^(r)`

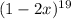
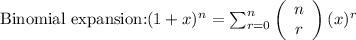
Using the binomial expansion, we get:

`\text{Binomial expansion: } (1 - 2x)^(19) = \sum_(r = 0)^(19)\left(\begin{array}{ccc}19\\r\end{array}\right) (-2x)^(r)`

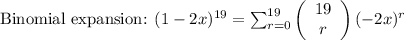
For the 15th term, we want the term where r is equal to 14, because of the fact that the first term starts when r = 0. Thus, for the 15th term, we need to include the 0th or the first term of the binomial expansion.

Thus, the fifteenth term is:

`\text{Binomial expansion (15th term):} \left(\begin{array}{ccc}19\\14\end{array}\right) (-2x)^(14)`