Question

How many intersections are there of the graphs of the equations below? x + 5y = 6 3x + 30y = 36

a. none
b. one
c. two
d. infinitely many

Answer 1

d) infinitely many

Hope this helped!

Answer 2

Answer: Option 'B' is correct.

Explanation:

Since we have given that

`x+5y=6\\\\and\\\\3x+30y=36`

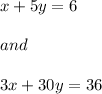
We need to find that " How many solutions are there ?"

First we compare the coefficients of x and y :

`a_1x+b_1y=c_1\\\\and,\\\\a_2x+b_2y=c_2`

Now,

`(a_2)/(a_1)=(b_2)/(b_1)=(c_2)/(c_1)`

Here,

`a_1=1,a_2=5,c_1=-6\\\\and\\\\a_2=3,b_2=30,c_2=36`

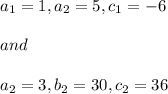
so, it becomes,

`(1)/(3)=(5)/(30)=(-6)/(-36)\\\\(1)/(3)\\eq (1)/(6)=(1)/(6)`

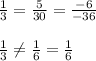
So, it becomes intersecting lines . So, they have unique solution.

Hence, Option 'B' is correct.