Question

As the distance of a sound wave from its source quadruples, how is the intensity changed?

Answer 1

d. it decreases by a factor of 16

Answer 2

The intensity decreases by a factor 16

Step-by-step explanation:

The intensity of a sound wave is inversely proportional to the square of the distance:

`I \propto (1)/(d^2)`

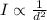
where

I is the intensity

d is the distance from the sound source

In this problem, we have that the distance from the source is quadrupled:

d' = 4 d

So, the new intensity will be:

`I' \propto (1)/(d'^2)=(1)/((4d)^2)=(1)/(16 d^2)=(I)/(16)`

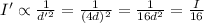
so, we see that the intensity has decreased by a factor 16.