Question

David drops a ball from a bridge at an initial height of 70 meters. (a) What is the height of the ball to the nearest tenth of a meter exactly 2 seconds after he releases the ball? (b) How many seconds after the ball is released will it hit the ground?

Answer 1

a) y (2) = 70 - 4.9 * 2^2 = 70 - 19.6 = 50.4 m
b) 0 = 70 - 4.9t^2
70/4.9=t^2
700/49 = t^2
10 √ 7/7 = t (in seconds)
t is approximately equal to 3.78 seconds

Answer 2

50.4 m is the height of the ball to the nearest tenth of a meter exactly 2 seconds after he releases the ball

3.78 seconds after the ball is released will hit the ground

Explanation:

Given : David drops a ball from a bridge at an initial height of 70 meters.

To Find: (a) What is the height of the ball to the nearest tenth of a meter exactly 2 seconds after he releases the ball? (b) How many seconds after the ball is released will it hit the ground?

Solution : Let y(t) denote the number of meters above the ground the ball is after t seconds,

Using equation of motion :

y(t) = 70 - ½gt²

Using g = 9.8 m/sec²,

we have y(t) = 70 - 4.9t² ----a

Thus (a) y(2) = 70 - 4.9 * 2² = 70 - 19.6 = 50.4 m

(b) how many seconds after the ball is released will it hit the ground

When ball hits the ground y will be 0

Putting value in equation a

0 = 70 - 4.9t²

`(70)/(4.9)= t^(2)`

`14.2857= t^(2)`

`√(14.2857) =t`

`3.779=t`

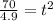
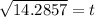
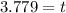
Thus t ≈ 3.78 sec

Hence 50.4 m is the height of the ball to the nearest tenth of a meter exactly 2 seconds after he releases the ball

3.78 seconds after the ball is released will hit the ground